算法之排序算法

发表于 2018-02-25 更新于 2025-12-11 分类于 Algorithm Waline：阅读次数：本文字数： 5.1k 阅读时长 ≈ 9 分钟

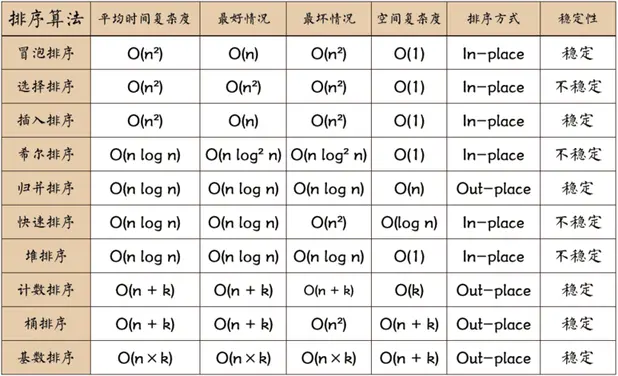
本文介绍基于一些数组的常用排序算法.

算法代码位置

稳定: 如果一个排序算法可以保持相同值的元素，相对位置不变，那么我们可以称这个排序算法是稳定的。
就地排序: 算法使用常量额外空间来生成输出（仅修改给定数组）。它仅通过修改列表中元素的顺序对列表进行排序。
内部和外部排序
- 当所有需要排序的数据不能一次放入内存时，排序称为外部排序。外部排序用于大量数据。
- 当所有数据都放在内存中时，排序称为内部排序。

冒泡排序

比较相邻的元素。如果第一个比第二个大，就交换它们两个；
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
针对所有的元素重复以上的步骤，除了最后一个；
重复步骤1~3，直到排序完成。

public static void bubbleSort(int[] arr) {
    int temp = 0;
    for (int i = arr.length - 1; i > 0; i--) { 
      // 每次需要排序的长度
        for (int j = 0; j < i; j++) { 
          // 从第一个元素到第i个元素
            if (arr[j] > arr[j + 1]) { // 此处是大于，相等的情况不交换位置
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

在相邻元素相等时，它们并不会交换位置，所以，冒泡排序是稳定排序。在数据完全有序的时候展现出最优时间复杂度，为 $O(n)$ 。其他情况下，几乎总是 $O(n^2)$ 。因此，算法在数据基本有序的情况下，性能最好。

要使算法在最佳情况下有 $O(n)$ 复杂度，需要做一些改进，增加一个swap的标志，当前一轮没有进行交换时，说明数组已经有序，没有必要再进行下一轮的循环了，直接退出。

public static void bubbleSort(int[] arr) {
    int temp = 0;
    boolean swap;
    for (int i = arr.length - 1; i > 0; i--) { 
        // 每次需要排序的长度
        swap=false;
        for (int j = 0; j < i; j++) { 
          // 从第一个元素到第i个元素
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swap=true;
            }
        }
        if (swap==false){
            break;
        }
    }
}

选择排序

在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
重复第二步，直到所有元素均排序完毕。

public static void selectionSort(int[] arr) {
    int temp, min = 0;
    for (int i = 0; i < arr.length - 1; i++) {
        min = i;
        // 循环查找最小值
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[min] > arr[j]) {
                min = j;
            }
        }
        if (min != i) {
            temp = arr[i];
            arr[i] = arr[min];
            arr[min] = temp;
        }
    }
}

用数组实现(就地排序)的选择排序是不稳定的，用链表实现(或者新开辟数组空间)的选择排序是稳定的。不过，一般提到排序算法时，大家往往会默认是数组实现(就地排序)，所以选择排序是不稳定的。

1
2
3

2a 2b 1 3
选择排序后 1 2b 2a 3
显然是不稳定的

插入排序

把待排序的数组分成已排序和未排序两部分，初始的时候把第一个元素认为是已排好序的。
从第二个元素开始，在已排好序的子数组中寻找到该元素合适的位置并插入该位置。
重复上述过程直到最后一个元素被插入有序子数组中。

public static void insertionSort(int[] arr){
    for (int i=1; i<arr.length; ++i){
        int value = arr[i];
        int position=i;
        while (position>0 && arr[position-1]>value){
            arr[position] = arr[position-1];
            position--;
        }
        arr[position] = value;
    }
}

由于只需要找到不大于当前数的位置而并不需要交换，因此，直接插入排序是稳定的排序方法。

二分插入排序

对于查询排序的优化可以通过，在选择插入位置时进行二分搜索优化。

把待排序的数组分成已排序和未排序两部分，初始的时候把第一个元素认为是已排好序的。
从第二个元素开始，在已排好序的子数组中寻找到该元素合适的位置并插入该位置(二分查询)。
重复上述过程直到最后一个元素被插入有序子数组中。

protected static void sort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        T target = array[i];
        if (array[i - 1] > target) {
            // 移动的位置
            int index = binarySearch(array, 0, i - 1, target);
            int j = i - 1;
            // 将比目标大的元素都向后移动一位
            while (j >= index) {
                // 稳定排序(等号)
                array[j + 1] = array[j];
                j = j - 1;
            }
            array[index] = target;
        }
    }
}
int binarySearch(int[] array, int beginIndex, int endIndex, int target) {
    if (beginIndex == endIndex) {
        return beginIndex;
    }
    int middle = (beginIndex + endIndex) / 2;
    if (array[middle] >target) {
        return binarySearch(array, beginIndex, middle, target);
    } else {
        return binarySearch(array, middle + 1, endIndex, target);
    }
}

希尔排序

希尔排序（Shell Sort）是插入排序的一种改进版本，也称为缩小增量排序。它通过将待排序的列表分成若干子列表，对每个子列表进行插入排序，逐步缩小子列表的间隔，最终完成整个数组的排序。

将数组按照gap = length /2 分组(0和 gap 是一组)，对每组进行插入排序。
缩小gap = gap / 2, 重复执行 1。直至 gap = 1

protected T[] sort(T[] array) {
        int len = array.length;
        T target = null;
        int j = 0;
        for (int gap = len / 2; gap >= 1; gap = gap / 2) {
            for (int i = gap; i < len; i++) {
                target = array[i];
                // 起始点 j
                j = i - gap;
                // 插入排序
                while (j >= 0 && comparator.compare(array[j],target) > 0) {
                    array[j + gap] = array[j];
                    j -= gap;
                }
                array[j + gap] = target;
            }
        }
        return array;
    }

希尔排序的时间复杂度取决于增量序列的选择：

最坏情况： $O(n^2)$ ，当增量序列选择不当时。
最好情况： $O(nlogn)$ ，当增量序列选择合适时。
平均情况： $O(nlogn)$ 到 $O(n^2)$ 之间。

常见的增量序列：

希尔增量： $\frac n 2$ , $\frac n 4$ , …, 1，时间复杂度为 $O(n^2)$ 。
Hibbard 增量：1, 3, 7, 15, …, $2^k - 1$ ，时间复杂度为 $O(n^{\frac 3 2})$ 。
Sedgewick 增量：1, 5, 19, 41, 109, …，时间复杂度为 $O(n^{\frac 4 3})$ 。

归并排序

归并排序有两种实现方式:

自顶向下-递归
自底向上-迭代

递归法（Top-down）

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

// 递归法
public static void mergeSort(int[] arr){
    int[] temp =new int[arr.length];
    internalMergeSort(arr, temp, 0, arr.length-1);
}
private static void internalMergeSort(int[] arr, int[] temp, int left, int right){
    //当left==right的时，已经不需要再划分了
    if (left<right){
        int middle = (left+right)/2;
        internalMergeSort(arr, temp, left, middle);          //左子数组
        internalMergeSort(arr, temp, middle+1, right);       //右子数组
        mergeSortedArray(arr, temp, left, middle, right);    //合并两个子数组
    }
}
// 合并两个有序子序列
private static void mergeSortedArray(int arr[], int temp[], int left, int middle, int right){
    int i=left;      
    int j=middle+1;
    int k=0;
    while (i<=middle && j<=right){
        temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
    }
    while (i <=middle){
        temp[k++] = arr[i++];
    }
    while ( j<=right){
        temp[k++] = arr[j++];
    }
    //把数据复制回原数组
    for (i=0; i<k; ++i){
        arr[left+i] = temp[i];
    }
}

因为我们在遇到相等的数据的时候必然是按子序列顺序“抄写”到辅助数组上的，所以，归并排序同样是稳定算法。归并排序在数据量比较大的时候也有较为出色的表现（效率上），但是，其空间复杂度O(n)使得在数据量特别大的时候（例如，1千万数据）几乎不可接受。而且，考虑到有的机器内存本身就比较小，因此，采用归并排序一定要注意。

迭代法（Bottom-up）

将序列每相邻两个数字进行归并操作，形成 $(n+1)/2$ 个子序列，排序后每个序列包含两/一个元素
若此时子序列数不是1个则将上述序列再次归并，形成 $(n+3)/4$ 个子序列，每个序列包含四/三个元素
重复步骤2，直到所有元素排序完毕，即子序列数为1

参考

[1] 十大排序算法总结
[2] 十大经典排序算法